Mengenal Matriks

Diantara beberapa tool yang dipakai di ilmu komputer, matriks atau matrix adalah yang paling sering dimanfaatkan. Setiap angka di dalam matriks, mewakili data untuk melakukan perhitungan matematika. Karena matematika adalah ilmu pokok dari ilmu komputer, maka kita wajib kenal dengan matriks.

Tak hanya di ilmu komputer, di bidang lain seperti mesin, fisika, matematika, dan bidang ilmu lainnya, seringkali menggunakan matriks. Matriks sangat penting karena dibutuhkan untuk komputasi atau perhitungan di dalam penelitian bidang-bidang itu.

Pertama kali saya belajar matriks itu waktu SMP. Matriks atau dalam bahasa Inggris, matrix, adalah sejumlah elemen yang tersusun dalam baris dan kolom. Semua elemennya dibungkus di dalam kurung siku atau square brackets. Seperti di gambar ini.

Sekarang perhatikan matriks sebelah kiri gambar di bawah ini. Setiap elemen di dalam matriks punya indeks yang menunjukkan posisi dari elemen. Indeks ini ditentukan berdasarkan posisi elemen terhadap baris dan kolom. Indeks baris dinotasikan \( m \) dan indeks kolom \( n \). Pada contoh di bawah, matriks \( A \) di sebelah kanan, memiliki elemen \( a \) di baris kedua dan kolom pertama \( a_{21} \) bernilai \( 6 \).

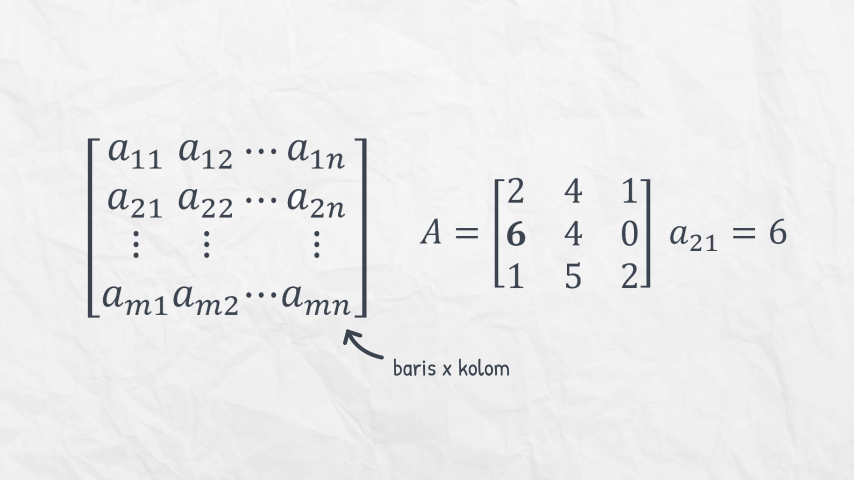
Matriks punya ukuran. Ukuran ini ditunjukkan oleh jumlah baris dan kolomnya. Kira-kira berapa ukuran matriks \( A \) di atas? Ukurannya \( 3 \times 3 \) karena terdiri dari \( 3 \) baris dan \( 3 \) kolom. Matriks \( A \) punya jumlah baris dan kolom yang sama, maka disebut matriks bujur sangkar atau square matrix. Matriks lainnya jika hanya punya satu kolom, disebut dengan vector atau vektor.

Nah, sekarang kita bahas beberapa tipe matriks.

Matriks Diagonal

Semua elemen yang diposisi baris dan kolom yang sama atau punya indeks \( m=n \), menunjukkan diagonal pada matriks. Matriks diagonal adalah matriks bujur sangkar yang setiap elemen pada indeks yang berbeda \( m\neq n \) selalu bernilai nol. Sedangkan semua elemen pada diagonal, bernilai bebas.

Kedua matriks di atas adalah matriks diagonal karena jumlah baris dan kolomnya sama dan semua elemen yang tidak berada di diagonal, bernilai nol.

Matriks Identitas

Matriks ini adalah matriks diagonal yang semua elemen di diagonal bernilai 1. Karena ini adalah matriks diagonal, maka matriks ini juga matriks bujur sangkar.

Matriks identitas biasanya dipakai di aljabar linear untuk menyelesaikan persamaan.

Matriks Segitiga

Matriks segitiga atau triangular matrix, terbagi menjadi dua tipe, yaitu matriks segitiga atas dan matriks segitiga bawah. Kalau semua elemen di atas elemen diagonal bernilai nol, maka disebut matriks segitiga atas. Dan sebaliknya, kalau semua elemen di bawah elemen diagonal bernilai nol, maka disebut matriks segitiga bawah.

Jika lupa mana yang matriks segitiga atas dan mana yang matriks segitiga bawah, amati elemen-elemen nol di bawah diagonal. Jika posisi elemen diatas diagonal, maka disebut matriks segitiga atas. Jika tidak, maka itu matriks segitiga bawah.

Matriks Transpose

Matriks ini didapat dari matriks lain yang ditukar kolom dengan barisnya.

Matriks \( C^T \) adalah matriks transpose dari matriks \( C \). Semua elemen di kolom pertama di matriks \( C \) menjadi elemen-elemen di baris pertama di matriks \( C^T \), dan semua elemen di kolom kedua di matriks \( C \) menjadi elemen di baris kedua di matriks \( C^T \).

Matriks Setangkup

Matriks setangkup atau symmetric matrix, adalah matriks yang elemen di atas diagonal dan dibawah diagonalnya adalah pasangan elemen yang kembar, dari hasil pencerminan terhadap diagonal.

Hati-hati kalau nentuin apakah sebuah matriks itu matriks setangkup atau bukan. Jika satu elemen aja ternyata tidak punya kembaran di bawah diagonal, maka matriks ini bukan matriks setangkup.

Matriks 01

Matriks 01 atau zero one matrix, adalah matriks yang hanya punya elemen angka 0 atau 1.

Posisi elemen nol atau satu bebas berada dimana saja. Mau di diagonal ataupun tidak, tidak masalah. Kalau semua elemen bernilai nol, maka tidak lagi disebut matriks 01, tapi menjadi matriks nol, atau zero matrix. Lain lagi kalau hanya ada satu elemen bernilai satu, dan lainnya nol, maka disebut single entry matrix.

Penulis

Rachmat Wahid Saleh Insani adalah seorang Dosen di Bidang Ilmu Komputer. Ia bergelar Master of Computer Science dari Universitas Gadjah Mada.