6 Langkah Melakukan Uji Hipotesis

Juni 30, 2020

Uji Hipotesis bertujuan untuk menentukan apakah ada bukti statistik yang cukup untuk mempercayai hipotesis terhadap suatu parameter. Artikel sebelumnya telah membahas tentang konsep dasar dari Uji Hipotesis. Sekarang kita akan membahas apa saja prosedur untuk melakukan Uji Hipotesis.

Baca juga: Mengenal Konsep Uji Hipotesis

Prosedur atau langkah untuk melakukan Uji Hipotesis melibatkan pemahaman tentang Significance Level, Statistik Uji, Aturan Keputusan, dan Critical Value of Z. Semuanya akan kita bahas di artikel ini.

#1 Memilih Bentuk Alternatif Hipotesis

Bentuk dari Alternatif Hipotesis atau Hypothesis Alternative ada tiga, yakni Upper-tailed Test, Lower-tailed Test, dan Two-tailed Test.

Seorang ahli statistika harus menentukan bentuk mana yang ia pilih berdasarkan apa yang ia percaya dari parameter yang sedang dibahas. Misalnya, suatu Hipotesis Null menyatakan bahwa Mean dari tinggi badan seluruh pemain basket di Indonesia adalah $ 181 $ sentimeter. Ahli statistika bebas ingin mempercayai apakah Mean dari tinggi badan mereka seharusnya lebih besar, kurang dari, atau bukan $ 181 $ sentimeter.

Jika ia mempercayai bahwa tinggi badan seluruh pemain basket seharusnya lebih dari $ 181 $ sentimeter sehingga dinyatakan $ H_1:\mu > \mu_0 $, maka bentuk Alternatif Hipotesis yang dipilih adalah Upper-tailed Test. Jika ia mempercayai kurang dari $ 181 $ sentimeter, yakni $ H_1:\mu < \mu_0 $, maka ia memilih Lower-tailed Test. Namun apabila ia mempercayai bahwa nilainya tidak sama dengan $ 181 $, yaitu $ H_1:\mu \neq \mu_0 $, maka bentuk yang ia pilih adalah Two-tailed Test.

Misalnya sang ahli statistika menyatakan bahwa seharusnya Mean dari tinggi badan seluruh pemain basket di Indonesia, lebih dari $ 181 $ sentimeter. Maka dinyatakan $ H_0: \mu = 191 $ dan $ H_1: \mu > 191 $.

Menentukan bentuk Alternatif Hipotesis adalah langkah pertama dalam melakukan Uji Hipotesis. Setelah itu menentukan besarnya $ \alpha $, yaitu Significance Level.

#2 Menentukan Significance Level

Significance Level, yaitu kemungkinan atau peluang kesalahan menolak Hipotesis Null yang ternyata bernilai benar. Berdasarkan contoh kasus skor ujian sebelumnya, Significance Level menunjukkan kemungkinan dari sang ahli statistika melakukan kesalahan, yaitu ia menolak Hipotesis Null yang menyatakan Mean tinggi badan sebesar $ 181 $ dan kenyataannya tinggi badan seluruh pemain basket di Indonesia memang benar sebesar itu.

Significance Level disimbolkan dengan alpha $ \alpha $, dan pada umumnya, nilainya sebesar $ 0.01, 0.05, $ atau $ 0.1 $. Seringkali ahli statistika memilih Significance Level sebesar $ 0.05 $ karena mereka beranggapan bahwa saat melakukan Uji Hipotesis nanti, kemungkinannya cukup besar bahwa nantinya terjadi suatu kesalahan oleh mereka. Hal ini sering dilakukan apabila sampel yang diobservasi adalah manusia.

Kita asumsikan saja sang ahli statistika memilih Significance Level sebesar $ 0.05 $.

#3 Memilih Statistik Uji

Setelah menentukan Significance Level, berikutnya memilih Statistik Uji atau Test Statistic, yaitu suatu nilai yang menyimpulkan informasi sampel. Contoh kasus yang sebelumnya, yakni skor ujian, bisa diasumsikan berbentuk Distribusi Normal dengan jumlah sampel yang besar. Oleh karena itu, Statistik Uji yang dipilih adalah Z-Test. Jika menggunakan sampel yang sedikit, bisa memilih T-Test.

Baca juga: Mempelajari Distribusi t-Student

Rumus Z-Test, diperoleh dari nilai Mean dari data sample dikurangi dengan nilai Mean dari hipotesis, lalu dibagi dengan Standard Error.

$$ Z=\frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}} $$

Pada contoh tinggi badan pemain basket ini, sang ahli statistika memilih 100 orang sebagai sampel. Oleh karena itu, Uji Statistik yang sesuai adalah Z-Test.

#4 Mengatur Aturan Keputusan

Kemudian kita menentukan Aturan Keputusan, yakni suatu pernyataan yang menunjukkan keadaan untuk menolak Hipotesis Null. Misalnya, Hipotesis Null ditolak jika nilai $ Z \geq 1.645 $. Aturan Keputusan ditentukan berdasarkan nilai tertentu dari Statistik Uji.

Jika bentuk Alternatif Hipotesis adalah Upper-tailed Test, maka Aturan Keputusannya adalah menolak Hipotesis Null jika Z-Test lebih besar dari statistik di Hipotesis Null. Pada Lower-tailed Test, Aturan Keputusan menolak Hipotesis Null jika Z-Test kurang dari statistik di Hipotesis Null. Sedangkan di Two-tailed Test, Aturan Keputusan menyatakan menolak Hipotesis Null saat Z-Test lebih besar atau kurang dari statistik di Hipotesis Null.

Jika Statistik Uji mengikuti Distribusi Normal, maka Aturan Keputusan akan mengikuti Distribusi Normal Baku. Sedangkan jika Statistik Uji mengikuti Distribusi T, maka Aturan Keputusan juga mengikuti Distribusi T.

Aturan Keputusan mendefinisikan Rejection Region, yakni suatu area di dalam distribusi yang menunjukkan Alternatif Hipotesis bernilai benar. Bentuk Rejection Region untuk setiap bentuk Alternatif Hipotesis berbeda-beda. Besarnya Rejection Region juga bergantung pada Significance Level dan Z-Test.

Significance Level menentukan critical value of Z, yaitu nilai yang akan diperbandingkan dengan hasil Z-Test. Perhatikan gambar berikut.

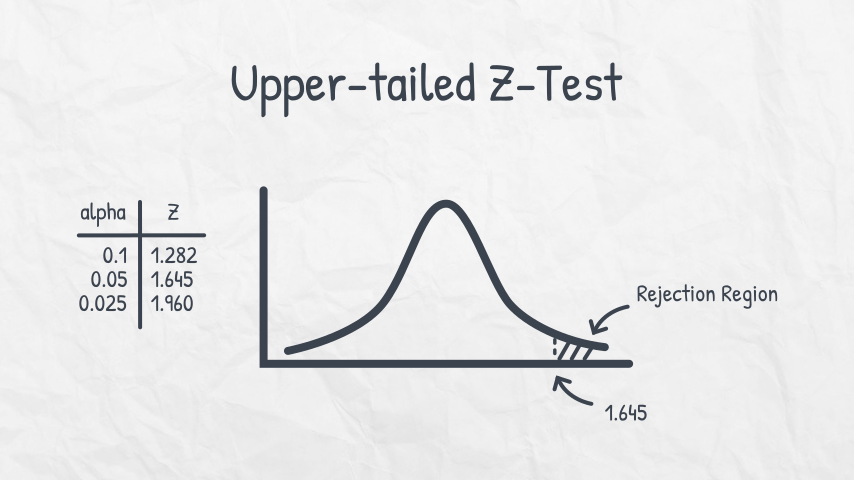
Setiap Critical Value of Z berpasangan dengan salah satu Significance Level.

Karena sang ahli statistika menentukan Significance Level sebesar $ 0.05 $ dalam Upper-tailed Test, maka di Aturan Keputusan, ia menolak $ H_0 $ jika $ Z \geq 1.645 $.

#5 Menghitung Statistik Uji

Pada langkah ini, lakukan perhitungan Statistik Uji dengan subtitusi data sampel yang diobservasi ke dalam Statistik Uji.

Hasil observasi dari tinggi badan pemain basket di Indonesia menunjukkan nilai Mean data sampel sebesar $ 195.3 $ dengan Standar Deviasi $ 25.6 $ dari banyaknya $ 100 $ sample adalah sebagai berikut.

$$ Z=\frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}=\frac{195.3-191}{\frac{25.6}{\sqrt{100}}}=2.38 $$

#6 Mengambil Kesimpulan

Kesimpulan diperoleh dengan membandingkan hasil Statistik Uji dengan Aturan Keputusan. Kesimpulan hanya ada satu diantara dua, yakni menolak Hipotesis Null atau tidak menolak Hipotesis Null.

Sang ahli statistika menolak $ H_0 $ karena $ 2.38 \geq 1.645 $. Selain itu, ia juga telah menunjukkan bahwa Mean dari tinggi badan seluruh pemain basket di Indonesia lebih dari $ 191 $ sentimeter.

Penulis

Rachmat Wahid Saleh Insani adalah seorang Dosen di Bidang Ilmu Komputer. Ia bergelar Master of Computer Science dari Universitas Gadjah Mada.

Anda mencari sesuatu? Cari disini!