Distribusi Normal Baku dan Cara Menghitungnya

Suatu kurva atau histogram yang membentuk Distribusi Normal untuk suatu variabel kemungkinan besar tidak sama persis dengan variabel lain. Ada yang lebih tinggi, ada yang lebih melebar dari yang lain. Parameter Distribusi Normal yang membuat bentuk kurva ini berbeda-beda walaupun tetap saja simetris.

Baca juga: Mendalami Distribusi Normal dan Aturan Empirisnya

Namun, ada suatu Distribusi Normal Baku, dimana parameternya, yakni nilai Mean, bernilai nol dan nilai Standar Deviasi-nya bernilai satu.

Apa pentingnya memahami Distribusi Normal Baku?

Sejumlah pengujian hipotesis dalam bidang statistika mengasumsikan bahwa data yang diperoleh akan membentuk Distribusi Normal. Selain itu, pada Teorema Limit Pusat atau Central Limit Theorem, dinyatakan bahwa semakin banyak sampel yang diperoleh, distribusi nilai mean dari sample (Distribution Sample of the Mean) cenderung membentuk Distribusi Normal.

Baca juga: Sampel dan Populasi: Apa Bedanya?

Apa itu Distribusi Normal Baku?

Distribusi Normal Baku juga disebut dengan Distribusi Z. Setiap nilai yang ada pada Distribusi Normal Baku ini disebut dengan istilah z-score atau Skor Standar. Angka pada z-score di Distribusi Normal Baku menunjukkan jumlah standar deviasi suatu observasi apakah jatuh di atas atau di bawah nilai Mean.

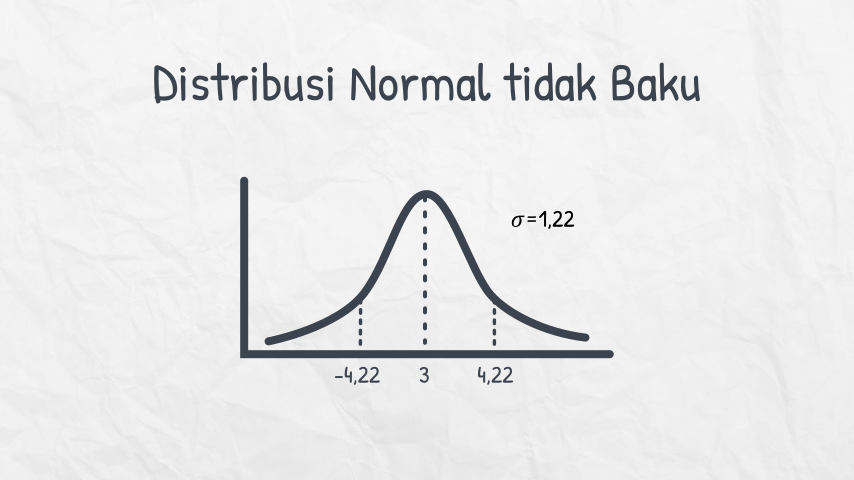
Pada kurva di atas, apakah merupakan Distribusi Normal Baku? Tentu tidak, karena nilai Mean-nya sebesar 3 dan nilai Standar Deviasinya adalah 1,22.

Baca juga: Teknik Visualisasi Data dalam Statistika

Ingat, nilai Mean pada Distribusi Normal Baku bernilai nol dan nilai Standar Deviasi-nya bernilai satu. Lalu bagaimana caranya membentuk Distribusi Normal Baku?

Bagaimana Caranya Menghitung Distribusi Normal Baku?

Sebelum mulai membuat Distribusi Normal Baku, kita harus menghitung nilai z-score terlebih dahulu. Nilai z-score dihitung dengan rumus berikut.

\( Z=\frac{x-\mu}{\sigma} \)

Rumus tersebut dapat dipahami lebih mudah dengan langkah-langkah di bawah ini:

1. Kurangi seluruh nilai data \( x \) dengan nilai Mean \( \mu \).
2. Lakukan pembagian seluruh hasil langkah pertama dengan nilai Standar Deviasi \( \sigma \).
3. Buatlah histogram berdasarkan hasil dari langkah kedua.

Apabila hasil dari perhitungan rumus tersebut digunakan untuk membangun histogram/kurva, maka akan terbentuk sebuah Distribusi Normal Baku.

Kurva di atas memiliki nilai Mean sebesar nol dan nilai Standar Deviasi sebesar satu. Oleh karena itu, histogram ini membentuk Distribusi Normal Baku.

Langkah-langkah yang baru saya kita bahas merupakan suatu proses standarisasi data. Proses standarisasi data membantu kita untuk membandingkan observasi-observasi yang diperoleh serta menghitung peluang antara populasi-populasi yang berbeda.

Bagaimana caranya membandingkan observasi diantara populasi yang berbeda?

Apa Manfaat dari Distribusi Normal Baku?

Perbandingan observasi dari populasi yang berbeda adalah salah satu hal yang bisa dilakukan dengan Distribusi Normal Baku. Selain itu, nilai z-score juga dapat membantu kita untuk melakukan ini.

Sebagai contoh, saya memiliki satu buah jeruk dan satu buah apel. Jika kedua buah ini diperbandingkan, apakah buah jeruk yang saya ambil lebih berat dari jeruk lainnya di pasar? Ataukah buah apel yang saya ambil adalah buah apel yang lebih berat dari buah apel lain di pasar?

Berat buah jeruk adalah 120 gram. Nilai rata-rata berat buah jeruk adalah 124 gram dengan nilai Standar Deviasi 10. Sedangkan berat buah apel adalah 110 gram. Nilai rata-rata berat buah apel adalah 120 gram dengan nilai Standar Deviasi 15.

Mari kita hitung nili z-score kedua buah ini.

Karena nilai z-score buah jeruk negatif, berarti jeruk yang saya ambil adalah buah jeruk yang lebih ringan dari kebanyakan jeruk lainnya. Sedangkan buah apel yang saya ambil lebih berat dari buah apel lain.

Kesimpulan

Apa saja pemahaman Distribusi Normal Baku yang sudah kita bahas di artikel ini?

• Distribusi Normal Baku memiliki nilai Mean sebesar nol, dan nilai Standar Deviasi sebesar satu.
• Distribusi ini dibentuk menggunakan z-score.
• Kita dapat membandingkan suatu observasi diantara beberapa populasi menggunakan nilai z-score.
• Menghitung nilai z-score disebut juga dengan istilah standardisasi data.

Penulis

Rachmat Wahid Saleh Insani adalah seorang Dosen di Bidang Ilmu Komputer. Ia bergelar Master of Computer Science dari Universitas Gadjah Mada.