Menemukan Ukuran Variabilitas Suatu Dataset
Anda sedang menganalisis data tinggi badan mahasiswa di sebuah kota. Setelah mengumpulkan data, Anda mendapatkan kesimpulan bahwa rata-rata tinggi badan mahasiswa adalah 160 cm. Apakah ini menunjukkan bahwa mahasiswa di kota tersebut tergolong memiliki tinggi badan yang pendek? Apakah tidak ada kemungkinan terdapat mahasiswa dengan tinggi badan 180 cm?
Pertanyaan-pertanyaan tersebut dapat dijawab dengan mengukur Variabilitas dari dataset Anda. Apa itu Variabilitas? Variabilitas adalah ukuran yang menunjukkan seberapa beragamnya data yang Anda analisis.
Lalu bagaimana caranya mengukur Variabilitas dari suatu dataset? Artikel ini akan membahas beberapa cara untuk mengukurnya. Cara pertama dengan menemukan nilai Rentang. Cara kedua dengan menemukan empat bagian yang sama dari dataset. Cara ketiga dengan menghitung nilai Variansi. Kemudian cara terakhir dengan menghitung nilai Standar Deviasi.
Mencari Selisih Nilai Data Tertinggi dengan Nilai Data Terendah
Banyaknya data yang ada diantara nilai data terendah dengan nilai data tertinggi disebut dengan istilah rentang (range). Selisih antara nilai data terendah dengan nilai data tertinggi adalah nilai rentang.
Sebagai contoh, seorang siswa mendapatkan uang jajan sebesar 2000 rupiah di hari pertama. Pada hari kedua dan ketiga, ia mendapatkan uang jajan sebesar 1000 dan 5000 rupiah. Maka nilai rentangnya ialah 4000 rupiah, selisih dari 1000 hingga 5000 rupiah.
Bagaimana cara menemukan rentang pada Histogram?
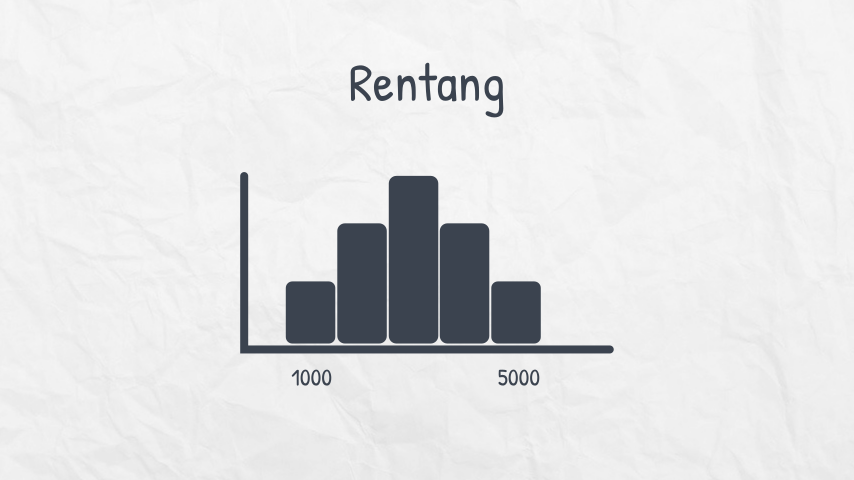
Pada histogram di atas, rentang dapat ditentukan dengan melihat sumbu horizontal. Nilai data terendah berada di bar pertama yang terletak di posisi paling kiri, yaitu 1000. Sedangkan nilai data tertinggi berada di bar paling kanan, yaitu 5000. Nilai rentang dataset ini adalah 4000.
Membagi Data Menjadi Empat Bagian
Seluruh dataset diurutkan dari yang nilainya terendah hingga tertinggi. Kemudian data dibagi menjadi empat bagian yang sama banyak, tiga nilai data yang menjadi potongan bagiannya disebut dengan istilah Kuartil (Quartile).
Empat kuartil yang diperoleh, diberi nama \(Q1\) untuk Kuartil Pertama atau Kuartil Bawah, \( Q2 \) untuk Kuartil Kedua atau Kuartil Tengah, dan \( Q3 \) untuk Kuartil Ketiga atau Kuartil Atas. Selisih antara \( Q3 \) dan \( Q1 \) adalah Interquartile Range (IQR) atau Simpangan Kuartil atau Jangkauan Semi Antar Kuartil. IQR menunjukkan \( 50 \) persen dataset yang berada di dalam distribusi data. Perhatikan gambar di bawah ini.
Pada gambar di atas, terlihat bahwa dataset sudah diurutkan dari nilai data terendah hingga tertinggi. Nilai \( Q1, Q2, Q3 \) pada dataset tersebut adalah \( 2,3,4 \). Maka, nilai IQR-nya adalah \( Q3-Q1=2 \).
Mengukur Seberapa Jauh Data Menyebar dari Titik Tengahnya
Variance atau Variansi adalah nilai yang menunjukkan seberapa jauh jarak data di dalam distribusi dengan nilai Median atas distribusi tersebut.
Bagaimana cara menemukan nilai Variansi?
Nilai Variansi dapat ditemukan dengan beberapa langkah yang mudah. Jika ingin menghitung nilai Variansi dari suatu data populasi, caranya adalah sebagai berikut:
- Temukan nilai Mean.
- Hitung selisih antara setiap nilai data di dataset dengan nilai Mean.
- Hitung hasil pangkat dua dari langkah kedua untuk setiap nilai data.
- Jumlahkan seluruh hasil dari langkah ketiga.
- Bagi hasilnya dengan banyak data.
Namun jika ingin menghitung nilai Variansi untuk data sampel, langkahnya adalah:
- Temukan nilai Mean dari data sampel
- Hitung selisih antara setiap nilai data di dataset dengan nilai Mean.
- Hitung hasil pangkat dua dari langkah kedua untuk setiap nilai data.
- Jumlahkan seluruh hasil dari langkah ketiga.
- Bagi hasilnya dengan nilai banyak data dikurangi satu.
Apa rumus mencari nilai Variansi?
Nilai Variansi untuk data populasi rumusnya adalah sebagai berikut:
$$ \sigma^2=\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N} $$
Simbol \( \sigma^2 \) adalah nilai Variansi untuk data populasi, \( x \) merupakan nilai dataset, \( \mu \) adalah nilai Mean untuk data populasi, dan \( N \) adalah banyaknya data populasi.
Langkah-langkah menghitung Variance untuk data populasi diperlihatkan oleh gambar di bawah ini.
Lalu apa rumus mencari nilai Variansi untuk data sampel? Rumus untuk Variansi data sampel dan data populasi tidak jauh berbeda.
$$ S^2=\frac{\sum_{i=1}^{n}\left(x_i-\bar{x}\right)^2}{n-1} $$
\( S^2 \) adalah perkiraan nilai Variansi untuk data sampel, \( x \) merupakan nilai setiap data, \( \bar{x} \) adalah nilai Mean untuk data sampel, dan \( n \) merupakan banyaknya data sampel.
Variansi dalam Histogram
Suatu dataset dapat memiliki nilai Mean yang sama dengan dataset lain. Namun, kedua dataset dapat memiliki nilai Variansi yang berbeda. Nilai Mean yang menunjukkan dimana nilai data berkumpul tidak dapat menunjukkan seberapa beragamnya data seperti yang bisa ditunjukkan oleh nilai Variansi. Perhatikan gambar di bawah ini.
Kedua histogram dibuat dari dua dataset yang berbeda. Nilai Mean keduanya sama, namun nilai Variansinya berbeda. Pada histogram yang berwarna biru, data terlihat lebih beragam jika dibandingkan dengan histogram yang berwarna kuning.
Menghitung Nilai Standar Deviasi
Nilai Standar Deviasi atau Standard Deviation dapat diperoleh dengan menghitung akar dari nilai Variansi. Nilai ini adalah selisih dari setiap nilai data dengan nilai Mean. Jika data berkumpul di suatu lokasi, maka nilai Standar Deviasinya kecil. Namun jika data menyebar, maka nilai Standar Deviasinya besar.
Kalau Standar Deviasi diperoleh hanya dengan menghitung akar dari Variansi, mengapa repot-repot menemukannya? Nilai Standar Deviasi memiliki satuan yang sama dengan nilai data, sedangkan nilai Variansi tidak.
Sebagai contoh, rata-rata tinggi badan mahasiswa di suatu kampus adalah 165 cm. Nilai Standar Deviasinya adalah sebesar 5 cm. Berdasarkan nilai Mean dan Standar Deviasi tersebut, dapat disimpulkan bahwa tinggi badan mahasiswa kampus itu berkisar antara 160 hingga 170 cm. Perhatikan satuan pada nilai Standar Deviasi, sama dengan satuan pada nilai data, bukan?
Penulis
Rachmat Wahid Saleh Insani adalah seorang Dosen di Bidang Ilmu Komputer. Ia bergelar Master of Computer Science dari Universitas Gadjah Mada.
Anda mencari sesuatu? Cari disini!


