Mengenal Distribusi Probabilitas

Ketika berkunjung ke kota Jakarta, hampir setiap hari saya menemukan kemacetan di sana. Kemacetan ini tidak hanya terjadi di jalan tertentu, tapi hampir di semua jalan yang saya lewati. Teman saya yang tinggal di sana mengatakan bahwa di rute yang selalu ia tempuh saat berangkat ke kantor, jalanan yang ia lalui seringkali terkena kemacetan.

Menurut Anda, berapa besar kemungkinan kemacetan akan muncul di jalan itu?

Pertanyaan ini sangat bisa dijawab apabila kita menguasai konsep distribusi, atau biasa disebut juga dengan distribusi probabilitas.

Apa itu Distribusi Probabilitas?

Distribusi probabilitas adalah suatu fungsi yang menunjukkan sejumlah nilai yang mungkin diperoleh (outcome/hasil) dari suatu variabel serta seberapa sering nilai tersebut muncul.

Sebagai contoh, dari sebuah dadu, berapa angka yang bisa muncul jika dadu dilempar dan jatuh?

Pada kasus ini, variabel yang menjadi fokusnya adalah dadu, sedangkan nilai yang mungkin diperoleh adalah angka pada dadu.

Sebuah dadu memiliki enam sisi yang menunjukkan suatu angka. Ada enam angka, satu, dua, tiga, empat, lima, dan enam. Berapa kemungkinan muncul angka satu? Nilai kemungkinannya \( \frac{1}{6} \), bukan? Lalu berapa kemungkinan muncul angka lainnya? Nilainya sama, \( \frac{1}{6} \).

Bagaimana dengan angka tujuh? Berapa kemungkinannya?

Nilai kemungkinannya nol, karena tidak mungkin muncul angka tujuh pada dadu. Nol adalah nilai kemungkinan untuk kemunculan angka lain selain satu, dua, tiga, empat, lima, dan enam.

Seluruh nilai kemungkinan ini dapat diilustrasikan di diagram batang berikut ini.

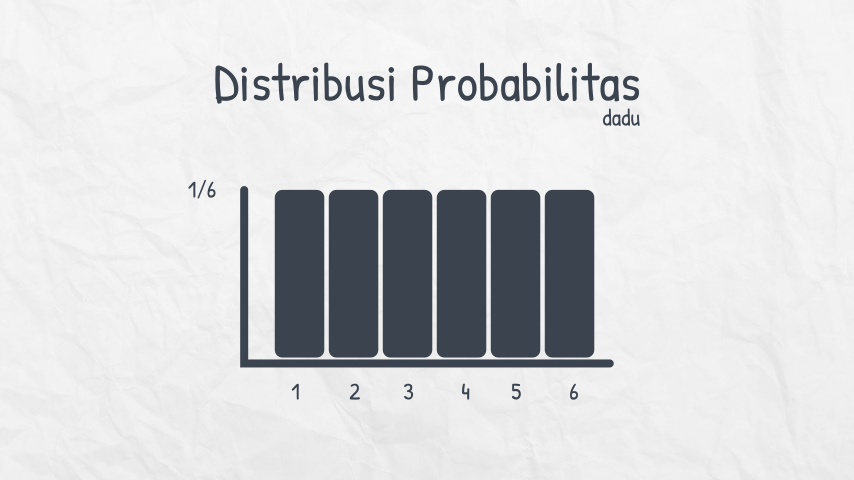
Baca juga: Teknik Visualisasi Data dalam Statistika

Diagram batang di atas adalah salah satu bentuk distribusi, yakni Uniform Distribution. Selain Uniform Distribution, ada beberapa tipe distribusi lainnya, yakni Normal Distribution, Binomial Distribution, dan masih banyak lagi.

Kesimpulannya, dari keenam angka tersebut, semuanya memiliki kemungkinan yang sama untuk muncul, yakni \( \frac{1}{6} \).

Nilai kemunculan atau probabilitas suatu outcome/hasil \( x \) dinotasikan dengan simbol \( p\left(x\right) \) atau \( P\left(x\right) \) atau \( Pr\left(x\right) \).

Total dari seluruh nilai kemunculan suatu variabel harus bernilai satu. Pada contoh dadu, apabila seluruh angka memiliki nilai kemungkinan \( \frac{1}{6} \), maka totalnya adalah \( 1 \). Karena ada enam angka, maka \( \frac{1}{6}\times6=1 \).

Distribusi probabilitas merupakan ringkasan dari probabilitas/kemungkinan dari nilai suatu variabel acak. Lalu apa itu variabel acak?

Variabel Acak

Variabel acak adalah data kuantitatif yang dihasilkan oleh suatu proses yang menghasilkan hasil atau outcome yang acak, atau bisa dibilang hasilnya tidak bisa ditebak. Satu atau beberapa nilai kemungkinan dari variabel acak disebut sebagai probabilitas.

Variabel acak dinotasikan dalam huruf kapital, misalnya \( X \). Nilai kemungkinan dari variabel acak ini dinotasikan dengan huruf kecil serta indeks, misalnya \( x_1,x_2,x_3 \). Maka berdasarkan contoh sebelumnya, \( X \) adalah dadu, dan \( \frac{1}{6} \) adalah \( x_1,x_2,x_3,x_4,x_5,x_6 \)

Sejumlah nilai-nilai yang mungkin menjadi nilai kemungkinan suatu variabel acak, disebut dengan domain. Nilai pada domain dapat berbentuk data diskrit ataupun data kontinu. Pada kasus dadu, domainnya adalah angka satu hingga enam yang merupakan data diskrit.

Variabel acak terdiri dari beberapa tipe, yakni:

• Variabel acak diskrit atau discrete random variable, contohnya warna mobil dan jumlah penduduk.
• Variabel acak boolean atau boolean random variable, seperti jenis kelamin.
• Variabel acak kontinu atau continuous random variable, misalnya suhu ruangan dan volume air.

Pada suatu Distribusi Probabilitas, ada beberapa properti atau nilai yang bisa diukur, yakni nilai mean, variansi, kemiringan, dan kurtosis.

Baca juga: Memahami Makna Kemiringan Suatu Dataset

Apabila kita mampu menentukan probabilitas suatu kejadian, maka kita bisa membuat prediksi atas kejadian ini di masa depan. Probabilitas adalah konsep yang penting dalam melakukan prediksi serta penilaian resiko.

Penulis

Rachmat Wahid Saleh Insani adalah seorang Dosen di Bidang Ilmu Komputer. Ia bergelar Master of Computer Science dari Universitas Gadjah Mada.